- ПРОМСТРОИТЕЛЬСТВО
- Строительство «под ключ», капитальный и текущий ремонт
- Геодезические изыскания
- Земляные работы
- Конструкции монолитные, железобетонные, металлические
- Ограждающие (стеновые и кровельные) конструкции
- Устройство кровель (наплавляемые, мембранные, металлические, система Kalzip)
- Инженерные сети
- Технологические трубопроводы, газопроводы, нефтепроводы, трубопроводы пара и горячей воды
- Технологическое оборудование (котлы, дробилки, конвейеры, мостовые краны)
- Механизмы вращения (турбины, насосы, дымососы, компрессоры)
- Градирни
- Насосные станции, станции химической и водоочистки
- Промышленная теплоизоляция (напыляемая, волокнистыми материалами)
- Футеровочные работы
- Обследование и инженерное сопровождение
- Авторский надзор
- Автоматизированные системы управления
- Строительство «под ключ», капитальный и текущий ремонт
- ЧИСТЫЕ ПОМЕЩЕНИЯ
- ПРОИЗВОДСТВО
- Металлоконструкции быстровозводимых сооружений
- Фасадная система ФРС
- Витражные системы VIDNAL, СИАЛ
- Реечные потолки
- Двери и окна ПВХ
- Двери металлические, двери противопожарные
- Изделия из нержавеющей стали
- Сложные тентовые конструкции пластичной архитектуры, крупномасштабные, легкие и мобильные
- Раскрой и сварка строительного текстиля (PVC, ETFE, PTFE, силиконовых тканей, тканей с тефлоновым покрытием)
- МЕТАЛЛООБРАБОТКА
GET A FREE QUOTE
Please fill this for and we'll get back to you as soon as possible!
- ИНЖИНИРИНГ
GET A FREE QUOTE
Please fill this for and we'll get back to you as soon as possible!
- ФАСАДЫ
- Навесные вентилируемые фасады
- Фасады проектирование, поставка материалов, монтаж, обслуживание
- Светопрозрачные конструкции (витражи, входные группы, окна, двери, зенитные фонари)
- ИНТЕРЬЕРЫ
- Современные интерьерные решения
- Лестницы и лестничные ограждения из нерж. стали и стекла
- Предметы интерьера из нерж. стали и черного металла по индивидуальным заказам
- Ограждение и облицовка атриумов, лифтов, эскалаторов, колонн, стоек ресепшн
- Отделочные работы с применением стекла, зеркал и металла
- Стеклянные перегородки с системой «DORMA»
- Подвесные потолки «Luxalon»
- Натяжные потолки и конструкции «BARRISOL» (акустические, светорассеивающие, зеркальные, 3D, многослойные изображения, TREMPO)
- Ударопрочные и пулестойкие светопрозрачные конструкции
- Общестроительные работы
- Полы:
- Устройство стяжки и полусухой стяжки
- Бетонирование полов
- Устройство сухих полов
- Устройство наливных самовыравнивающих полов
- Устройство линолеума, ковролина, ПВХ плит, ламината, паркетной доски, эпоксидных полов, деревянных полов
- Укладка керамогранита, мозайки, мрамора, гранита
- Реставрация мрамора и гранита, шлифовка и полировка
- Стены:
- Кладка стен из кирпича, бетонных блоков, пазогребневых блоков, керамзитобетонных блоков, газобетонных блоков, паротерм, стеклянных блоков
- Монтаж перегородок и облицовка стен из ГКЛ, монтаж деревянных перегородок, звукоизоляция стен
- Штукатурка стен цементно-песчаным раствором, гипсовыми смесями, штукатурки типа «Короед»
- Подготовка под окраску, под обои, под декоративную штукатурку
- Окраска, оклейка обоями, нанесение декоративных штукатурок (венецианские, имитация ткани, кожи, дерева и др.)
- Облицовка стен мрамором, гранитом, плиткой, мозаикой, клинкерной плиткой, гипсовой плиткой
- Реставрация мрамора и гранита, шлифовка и полировка
- Обшивка стен имитацией бруса, имитацией бревна, вагонкой
- Потолки:
- Полы:
- Современные интерьерные решения
- ПОЖАРНАЯ БЕЗОПАСНОСТЬ
- Обеспечение пожарной безопасности зданий и сооружений
- Огнезащитная обработка строительных конструкций зданий и сооружений
- Разработка проекта по огнезащите
- Расчет объекта по огнезащите с выбором оптимального решения
- Пересогласование проекта
- Шефмонтаж по огнезащите
- Поставка огнезащитных материалов по всем типам поверхности
- Проектирование охранно-пожарной сигнализации
- Монтаж и пуско-наладка систем ОПС
- Монтаж и пуско-наладка систем оповещения и видеонаблюдения
- Противопожарные светопрозрачные конструкции
- Витражи, входные группы, окна, двери, зенитные фонари, интерьерные светопрозрачные перегородки, сан.тех. перегородки
- Обеспечение пожарной безопасности зданий и сооружений

Kallyas is an ultra-premium, responsive theme built for today websites.
Тел.: +7 (383) 325-02-14,
Тел.: +7 (913) 000-33-22
Email: info@otlcom.com
ООО "Отличная компания"
630015, Россия, г. Новосибирск, ул. Алейская, 6, корпус 5, офис 25
Расчеты конструкций с помощью математических моделей и численных методов (Метод Конечных Объемов, Метод Конечных Элементов):

Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.
Идея метода
Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.
Если говорить в матричных терминах, то собираются так называемые матрицы жёсткости (или матрица Дирихле) и масс. Далее на эти матрицы накладываются граничные условия (например, при условиях Неймана в матрицах не меняется ничего, а при условиях Дирихле из матриц вычёркиваются строки и столбцы, соответствующие граничным узлам, так как в силу краевых условий значение соответствующих компонент решения известно). Затем собирается система линейных уравнений и решается одним из известных методов.
С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.
Иллюстрация метода на одномерном примере

Функция на H 0 1 , {\displaystyle H_{0}^{1},} с нулевыми значениями на концах (голубая), и аппроксимация этой функции отрезками (красная).
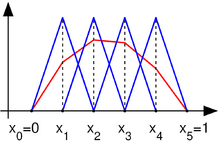
Базисные функции vk (голубые) и линейная комбинация из них, которая аппроксимирует искомую функцию (красная).
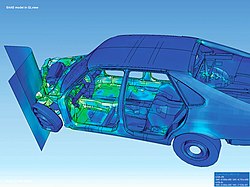
Визуализация деформации машины при асимметричном ударе, используя метод конечных элементов.
Пусть в одномерном пространстве Р1 необходимо решить следующее одномерное дифференциальное уравнение для нахождения функции u {\displaystyle u} на промежутке от 0 до 1. На границах области значение функции u {\displaystyle u} равно 0:
- P1 : { u ″ ( x ) = f ( x ) in ( 0 , 1 ) , u ( 0 ) = u ( 1 ) = 0 , {\displaystyle {\mbox{ P1 }}:{\begin{cases}u''(x)=f(x){\mbox{ in }}(0,1),\\u(0)=u(1)=0,\end{cases}}}
где f {\displaystyle f} известная функция, u {\displaystyle u} неизвестная функция от x {\displaystyle x} . u ″ {\displaystyle u''} вторая производная от u {\displaystyle u} по x {\displaystyle x} . Решение поставленной задачи методом конечных элементов разобьём на 2 этапа:
- Переформулируем граничную задачу в так называемую слабую (вариационную) форму. На этом этапе вычислений почти не требуется.
- На втором этапе разобьём слабую форму на конечные отрезки-элементы.
После этого возникает проблема нахождения системы линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.
Если u {\displaystyle u} есть решение, то для любой гладкой функции v {\displaystyle v} , которая удовлетворяет граничным условиям v = 0 {\displaystyle v=0} в точках x = 0 {\displaystyle x=0} и x = 1 {\displaystyle x=1} , можно записать следующее выражение:
(1) ∫ 0 1 f ( x ) v ( x ) d x = ∫ 0 1 u ″ ( x ) v ( x ) d x . {\displaystyle \int _{0}^{1}f(x)v(x)\,dx=\int _{0}^{1}u''(x)v(x)\,dx.}
С помощью интегрирования по частям преобразуем выражение (1) к следующей форме:
(2) ∫ 0 1 f ( x ) v ( x ) d x = ∫ 0 1 u ″ ( x ) v ( x ) d x = u ′ ( x ) v ( x ) | 0 1 − ∫ 0 1 u ′ ( x ) v ′ ( x ) d x = − ∫ 0 1 u ′ ( x ) v ′ ( x ) d x = − ϕ ( u , v ) . {\displaystyle {\begin{aligned}\int _{0}^{1}f(x)v(x)\,dx=\int _{0}^{1}u''(x)v(x)\,dx\\=u'(x)v(x){\bigg |}_{0}^{1}-\int _{0}^{1}u'(x)v'(x)\,dx\\=-\int _{0}^{1}u'(x)v'(x)\,dx=-\phi (u,v).\end{aligned}}}
Оно получено с учётом того, что v ( 0 ) = v ( 1 ) = 0 {\displaystyle v(0)=v(1)=0} .
Разобьём область, в которой ищется решение
- u ∈ H 0 1 {\displaystyle u\in H_{0}^{1}} такое, что
- ∀ v ∈ H 0 1 , − ϕ ( u , v ) = ∫ 0 1 f ( x ) v ( x ) d x {\displaystyle \forall v\in H_{0}^{1},\;-\phi (u,v)=\int _{0}^{1}f(x)v(x)dx}
на конечные промежутки, и получим новое пространство V {\displaystyle V} :
- (3) u ∈ V {\displaystyle u\in V} такое, что
- ∀ v ∈ V , − ϕ ( u , v ) = ∫ 0 1 f ( x ) v ( x ) d x {\displaystyle \forall v\in V,\;-\phi (u,v)=\int _{0}^{1}f(x)v(x)dx}
где V {\displaystyle V} кусочная область пространства H 0 1 {\displaystyle H_{0}^{1}} . Есть много способов для выбора базиса V {\displaystyle V} . Выберем в качестве базисных функций такие v k {\displaystyle v_{k}} , чтобы они представлялись прямыми линиями (полиномами первой степени):
- v k ( x ) = { x − x k − 1 x k − x k − 1 , x ∈ [ x k − 1 , x k ] , x k + 1 − x x k + 1 − x k , x ∈ [ x k , x k + 1 ] , 0 , x ∉ [ x k − 1 , x k + 1 ] {\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\mbox{, }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\mbox{, }}x\in [x_{k},x_{k+1}],\\0&{\mbox{, }}x\not \in [x_{k-1},x_{k+1}]\end{cases}}}
для k = 1 , … , n − 1 {\displaystyle k=1,\ldots ,n-1} (в данном примере n = 5 {\displaystyle n=5} )
Если теперь искомое приближённое решение представить виде u ( x ) = ∑ k = 1 n − 1 u k v k ( x ) {\displaystyle u(x)=\sum _{k=1}^{n-1}u_{k}v_{k}(x)} , а функцию f ( x ) {\displaystyle f(x)} аппроксимировать как f ( x ) = ∑ k = 0 n f k v k ( x ) {\displaystyle f(x)=\sum _{k=0}^{n}f_{k}v_{k}(x)} , то с помощью (3) можно получить следующую систему уравнений относительно искомых u k {\displaystyle u_{k}} :
- − ∑ k = 1 n − 1 u k ϕ ( v k , v j ) = ∑ k = 0 n f k ∫ v k v j d x {\displaystyle -\sum _{k=1}^{n-1}u_{k}\phi (v_{k},v_{j})=\sum _{k=0}^{n}f_{k}\int v_{k}v_{j}dx} ,
где j = 1 , … , n − 1 {\displaystyle j=1,\ldots ,n-1} .
Преимущества и недостатки
Метод конечных элементов сложнее метода конечных разностей в реализации. У МКЭ, однако, есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.
Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.





















![{\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\mbox{, }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\mbox{, }}x\in [x_{k},x_{k+1}],\\0&{\mbox{, }}x\not \in [x_{k-1},x_{k+1}]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8fcbd2a3dc976b13981291b89a48837f0f25598)







